Временные ряды и поиск иголки в стоге сена

Я расскажу о базовом инструменте анализа временных рядов — автокорреляционной функции. Однако в отличие от методов сглаживания, которые мы рассмотрели в первой части, этот инструмент анализа несколько по-иному обрабатывает ряд. Также мы увидим, как идеи автокорреляции применяются для решения пары специфических задач.

Автокорреляция

Алгоритм построения автокорреляционной функции достаточно прост:

• Берутся две копии исходного ряда.
• Для каждой копии из значений вычитается среднее значение ряда.
• Копии выравниваются, после чего между собой перемножаются значения, соответствующие одинаковым точкам во времени.
• Результаты перемножения суммируются. Полученный результат (пока ненормализованный) является коэффициентом корреляции для смещения 0(обозначим как corr(0)).
• Копии ряда сдвигаются друг относительно друга на один шаг по времени. Вычисления повторяются. Получился результат для смещения 1.
• Вычисления повторяются для всей длины ряда, увеличивая смещение.

Получившееся множество коэффициентов корреляции для различных смещений и есть автокорреляционная функция. В заключение все коэффициенты делятся на коэффициентcorr(0), чтобы нормировать функцию так, что коэффициент для смещения 0 становится равен 1.

Компактно алгоритм описывается следующим образом:

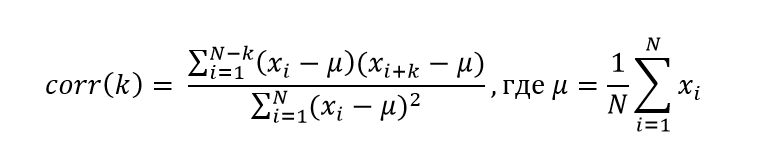
Функция автокорреляции имеет следующий смысл. Изначально два ряда полностью выровнены (смещение 0) и корреляция равна 1. Далее, когда мы начинаем сдвигать ряды, они постепенно «рассинхронизируются», значение корреляции падает.

Скорость падения говорит нам о том, насколько хорошо ряд «помнит» свои предыдущие значения. Если корреляция падает быстро с ростом смещения, ряд быстро «забывает» предыдущие значения. Если корреляция падает медленно, мы имеем дело с относительно устойчивым процессом во времени.

Возможны ситуации, когда функция быстро спадает, а затем снова растёт, образуя один или несколько пиков. Это означает, что ряды вновь начинают совпадать, если их сместить друг относительно друга на достаточное смещение по времени. То есть исходный ряд демонстрирует периодичность (сезонность). Количество шагов по времени, которому соответствует пик функции автокорреляции, соответствует периоду.

То есть функция описывает сходство между двумя рядами как функцию от разницы во времени между ними.

Вооружившись автокорреляцией, попробуем определить период для нашего первого ряда, описывающего объем авиаперевозок (http://robjhyndman.com/tsdldata/data/airpass.dat, источник Time Series Data Library, R. J. Hyndman. Ряд описывает количество пассажиров международных авиалиний в месяц (в тысячах) за период с 1949 по 1960 года).

Однако есть один момент применения автокорреляции. Метод есть смысл применять только для рядов, которые не содержат тренда и имеют среднее значение, равное нулю. Это связано с тем, что если ряд демонстрирует тренд и имеет ненулевое среднее (например, все значения достаточно большие и всё время растут, как в нашем примере), функция автокорреляции уловит эти особенности и будет воспринимать их как наличие у ряда «памяти», показывая наличие корреляции почти для всех смещений.

Есть два способа обойти проблему наличия тренда в наших данных:

• Вычесть тренд (т.е. выполнить детрендирование).
• Вместо исходного ряда построить ряд разностей соседних точек.

Вычесть тренд достаточно легко, но сначала его нужно оценить. Построение ряда разностей также полностью убирает тренд в данных.

После того, как тренд скомпенсирован, нам остается только поточечно вычесть среднее значение.

Все эти манипуляции легко выполнить в Prognoz Platform, причём с помощью интересного инструмента – калькулятора рядов. Калькулятор позволяет работать с рядами как с векторами значений, складывая и вычитая их, прибавляя константы, умножая на различные коэффициенты, применяя разные вычислительные методы. Его прелесть в том, что функции можно комбинировать, причём все преобразования недеструктивны – наш исходный ряд остаётся нетронутым.

Попробуем оценить линейный тренд для нашего ряда, и вычесть его, используя в качестве примера уже знакомый ряд с объёмами международных авиаперевозок. Для этого в инструменте анализа временных рядов, в калькуляторе рядов построим следующее выражение:

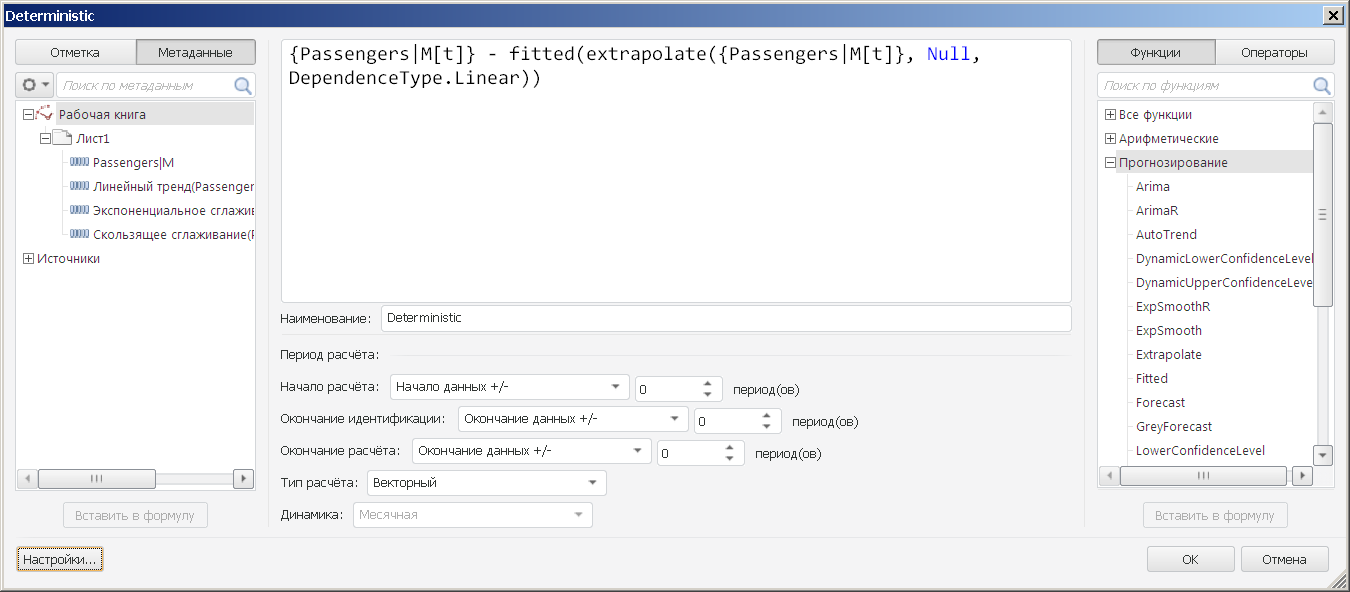
То есть сначала вычисляется ряд с линейным трендом, используя функцию Extrapolate (экстраполяция с подбором зависимости). Затем из исходного ряда вычитается тренд. Функция Fitted (подобранная зависимость) возвращает компонент, соответствующий именно тренду, т.к. помимо него Extrapolate возвращает ещё и ряд остатков (как и многие другие методы). Ниже я вывел графики исходного ряда, тренда, и детрендированного ряда.

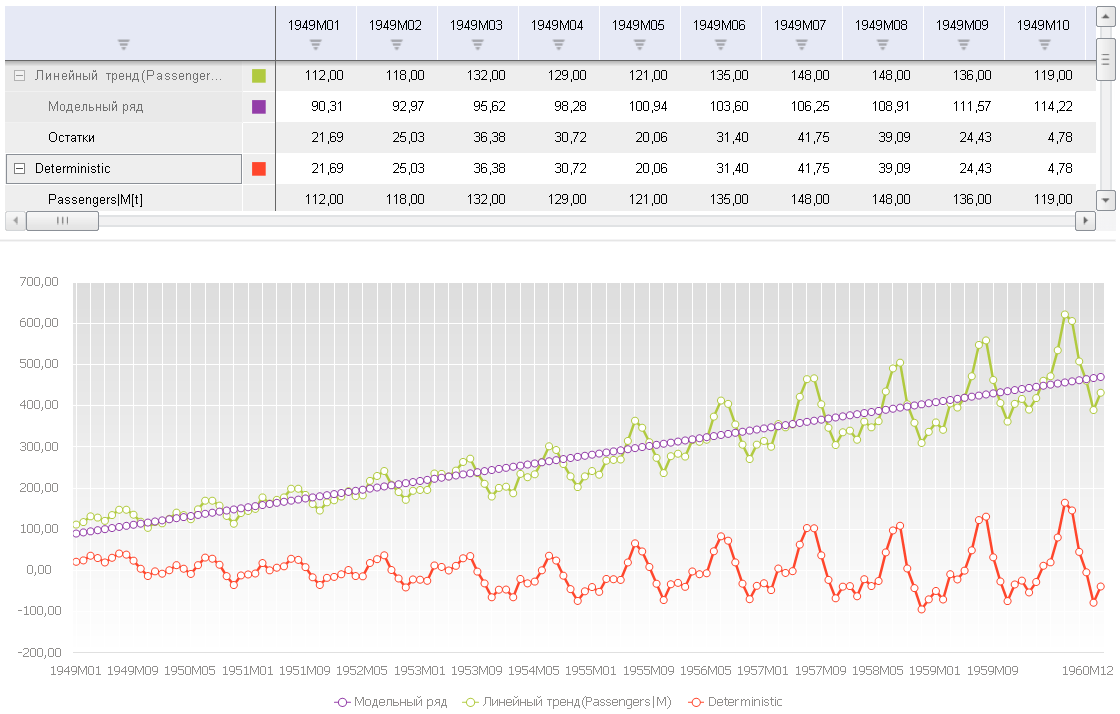
Чтобы оценить среднее у полученного ряда, вызовем для него команду «Статистика»:

То есть наш ряд после вычитания тренда и так уже имеет среднее, равное нулю.

Теперь мы можем вычислить функцию автокорреляции. Однако для этого нам потребуется использовать другой инструмент Prognoz Platform –Modeling & Forecasting («Моделирование и прогнозирование»), так как в инструменте анализа временных рядов функция автокорреляции недоступна. В инструменте Modeling & Forecasting нужно вызвать команду «Статистические характеристики», выбрать опцию «АКФ», указать ряд, для которого нужно выполнить расчёт, и указать преобразование ряда – линейное детрендирование. После расчёта мы получим следующую функцию:

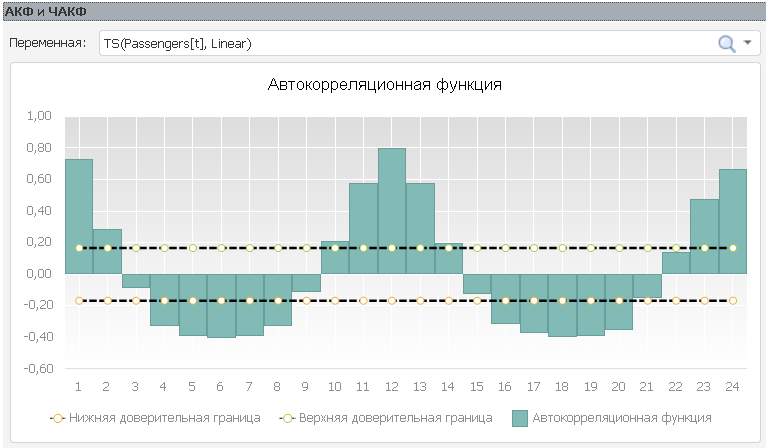
Как мы видим, функция быстро спадает, но на смещении 12 появляется самый большой пик. Это говорит о том, что наш ряд имеет периодичность, равную 12 месяцам. То есть если бы, например, сотрудники авиакомпании или аэропорта анализировали бы подобный ряд, описывающий их пассажиропоток, то выявив периодичность в 12 месяцев, компания могла бы сделать вывод, что распределение пассажиров по месяцам в наступающем году будет соответствовать уходящему году. Это, в свою очередь, будет влиять на затраты и выручку компании в каждый период. А используя метод экспоненциального сглаживания, компания может построить ещё более точный прогноз. При этом методы весьма просты.

Поиск иголки в стоге сена

Подход, используемый функцией автокорреляции, можно использовать для поиска «иголки» в «стоге сена». Путь нашей «иголкой» будет фрагмент аудиозаписи, а «стогом сена» – длинная запись, содержащая где-то внутри себя искомый фрагмент.

Звуковой сигнал можно описать как изменение амплитуды во времени. То есть это тоже временной ряд, только частота снятия значений амплитуды очень велика (десятки и сотни тысяч значений в секунду).

Допустим, мы имеем два аудиофрагмента u и v:

Простой способ сравнить их – посчитать величину скалярного произведения:

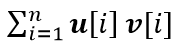
Чем более похожи будут два наших вектора, тем больше будет произведение, то есть почти идентичные аудиозаписи покажут большее значение, чем различающиеся.

Таким образом, мы можем сопоставлять наш искомый фрагмент с полной записью и считать величину скалярного произведения. После этого сдвинуть фрагменты друг относительно друга и вновь посчитать произведение, и т.д.

Позиция, соответствующая самой большой величине, будет позицией начала фрагмента, наиболее похожего на искомый.

Однако представьте, что наш «стог» содержит миллионы элементов, а наша иголка – десятки тысяч. То есть нам придётся вычислить миллионы скалярных произведений. Этот процесс крайне ресурсоёмкий. Однако существуют методы, позволяющие быстро вычислить сразу все подобные произведения, но они уже достаточно сложны.

Автокорреляция и современная поп-музыка

Интересный пример использования автокорреляции – фильтрация голосов исполнителей с использованием алгоритма Auto-tune («Автоматическая настройка»). Идея в том, что когда мы слышим музыку и пение, мы воспринимаем звучание как гармоничное, если тона всех инструментов и голоса исполнителя совпадают.

Однако «неопытные» исполнители часто делают ошибки и не попадают в нужную тональность. Чтобы сократить количество перезаписей песни, как раз и применяется Auto-tune. Этот алгоритм позволяет почти незаметно скорректировать тональность голоса исполнителя до ближайшего полутона (интервал между двумя соседними клавишами на фортепиано). Некоторые исполнители используют Auto-tune и на живых концертах.

Но для того, чтобы скорректировать тон голоса на выходе, сначала нужно вычислить этот тон (его высоту).

Это можно сделать двумя способами:

- Используя принцип поиска «иголки» в «стоге сена», пытаться сопоставить сигнал голоса с одой из нот. Этот метод не так быстр, как хотелось бы.

- Используя автокорреляцию, вычислить период колебаний, а зная его, вычислить высоту тона. Именно этот метод используют в коммерческих реализациях.

Один из производителей подобной аппаратуры в документации указывает, что алгоритм позволяет вычислить период колебаний всего по паре циклов сигнала, когда слушатель ещё даже не начал воспринимать его, за сотые доли секунды. При этом точность определения высоты тона достигает десятитысячных Герца. Ошибка коррекции до ближайшего полутона не превышает 1%. По-моему, очень неплохие показатели.

Я предлагаю вам послушать песню, в которой Auto-tune был применён впервые, в 1998 году. Однако певица Шер использовала его для художественного эффекта, а не для корректировки исполнительских ошибок. Вы сможете услышать эти фрагменты, когда тональность голоса резко модулируется, он начинает звучать неестественно, с «металлическим» оттенком. Особенно часто эффект появляется в последние полминуты. Но это пример «экстремального» использования. Обычно работу алгоритма практически не заметно. Удачно получилось у Шер или нет, судить вам!